Wordle: What's the Best Starting Word?

Over the holidays, my fiancée's family and I were obsessed with the word game Wordle. It's a simple game where you get six chances to guess a daily hidden word. Each guess gives you more information on what characters were correct, which were right but in the wrong position, and incorrect.

Immediately, I wondered – what was the optimal first guess? Should you include lots of vowels? Or strategically eliminate letters? Luckily, this seems like a programming brain teaser.

After crunching the numbers, the best starting word for Wordle is ...

How did I get there? I had solved a similar problem years ago for a similar game my friend developed called Word Joust. The game was like Wordle, except you played against an opponent and tried to guess their word. Here's my GitHub repository from then.

First, I thought I'd look at letter frequencies. Which letters show up the most, and in which positions? But, from my lessons in Coding Classical Latin, sometimes the best solution is simply a brute force solution. While a min-max algorithm might work here, I didn't have the time or the patience to code it up. So I choose a more straightforward solution.

Greedily minimize the number of remaining solutions with each guess.

To figure out the best starting word, I looked at which word eliminated the highest amount of possible solutions. This strategy should work because each guess is independent of the other. Picking the greediest solution each round should yield the most information. From each guess, you can learn three things:

1. Correct letters in the right position. Eliminate all words that do not have the letter in the same position.
2. Mismatched letters. Eliminate all the words that do not contain that letter in any position. Also, eliminate words that have the letter in that position.
3. The count of letters. This one is trickier. Let's say our guess was brass , and the hidden word is trash. In the fourth position, our letter would be green (correct and in the correct position). However, the second 's' would be greyed out (incorrect). This tells us that the solution only has 1 's.' We can eliminate all words with either 0 or more than 1 's.'

So the algorithm is three-part – figure out the match results, incorporate new information, and filter impossible solutions.

Second, we'll need to know what word lists to use. Again, looking through the source code of Wordle reveals two lists – a valid guess list (12972 words) and a valid solution list (2315 words). This hard-coded guess and solution list is probably because the developers didn't want the Wordle of the day to be an obscure word.

Figuring out the best first word is simply running the algorithm over each (guess, solution) pair and averaging the filtered words by guess. Here's a chart of the results. (It took about 20 minutes to run my messy, unoptimized code on my laptop).

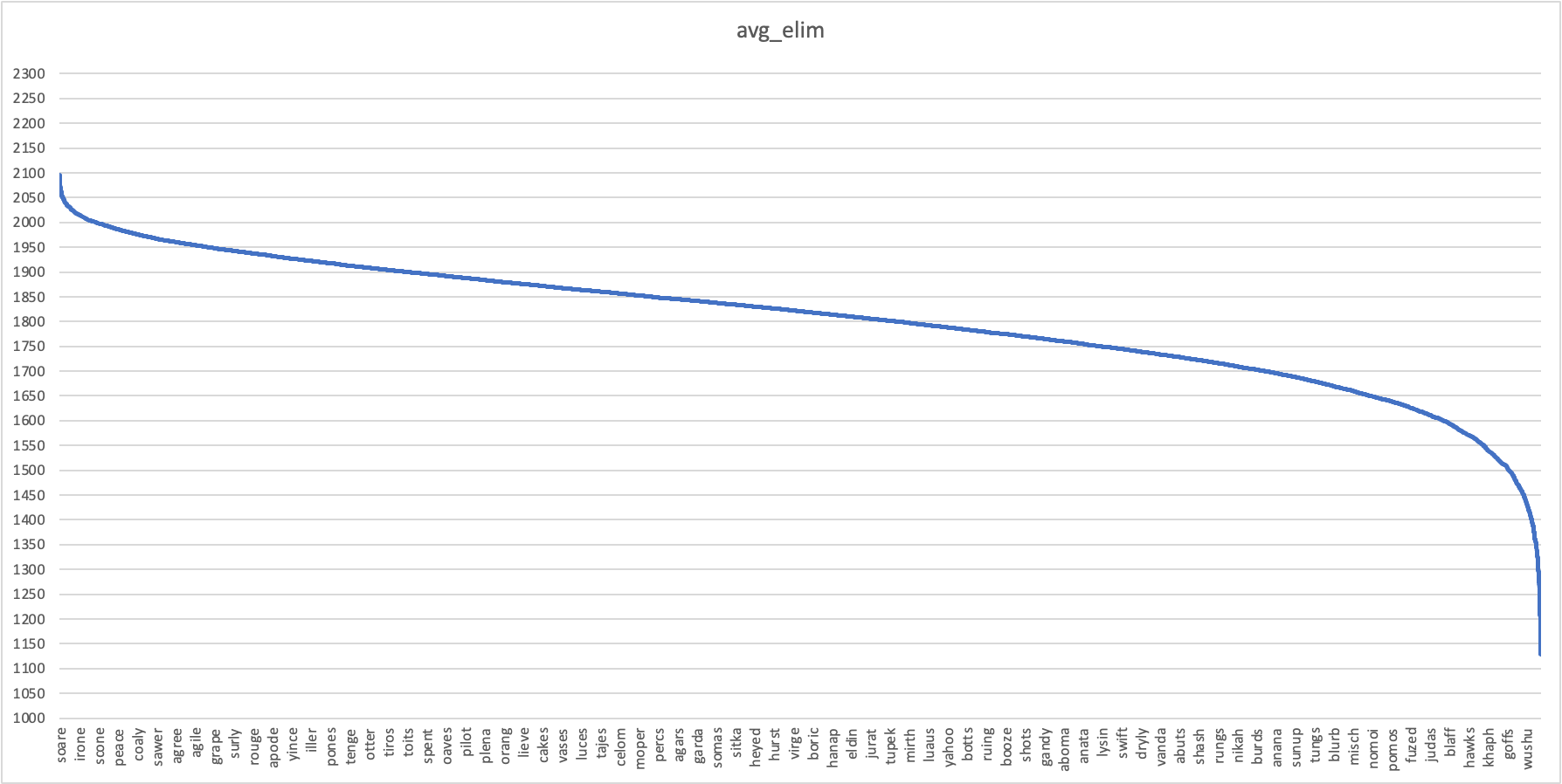
Guessing SOARE as your first word leaves an average of only 219 possible solutions. Meanwhile, some of the worst words to guess are JUJUS (1186 words left on average) and FUFFS (1143).

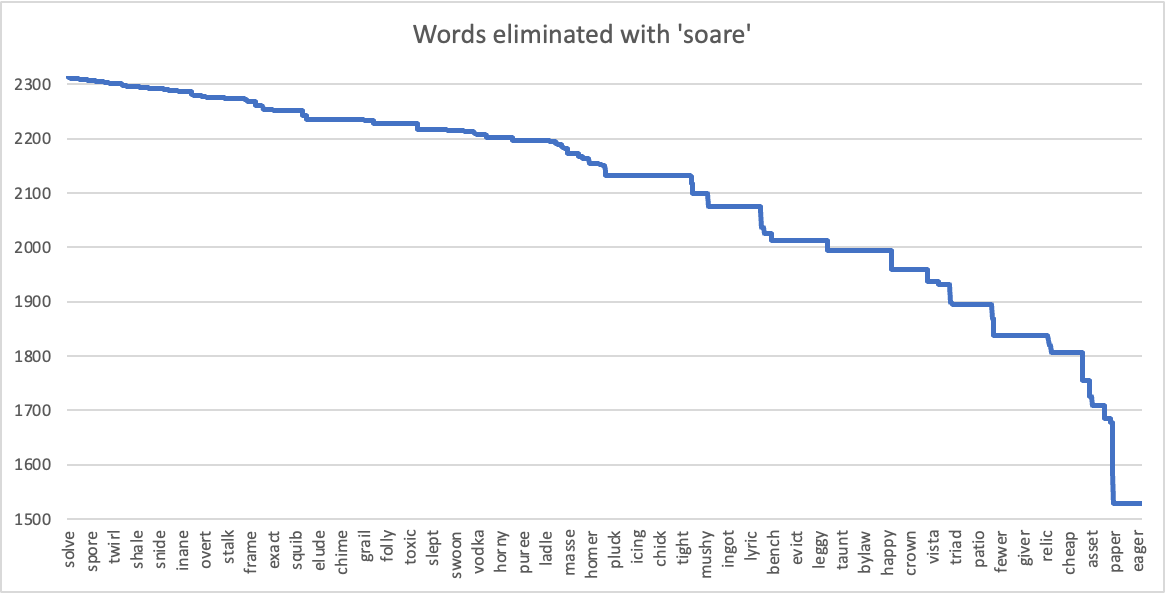
Looking at SOARE, you can see the number of eliminated words for each possible solution. For solutions like SOLVE, SORRY, and SOAPY, this guess eliminates all other possibilities. Even in the worst case (FERAL, ANGER), this guess eliminates almost half of the possible solutions (1529).

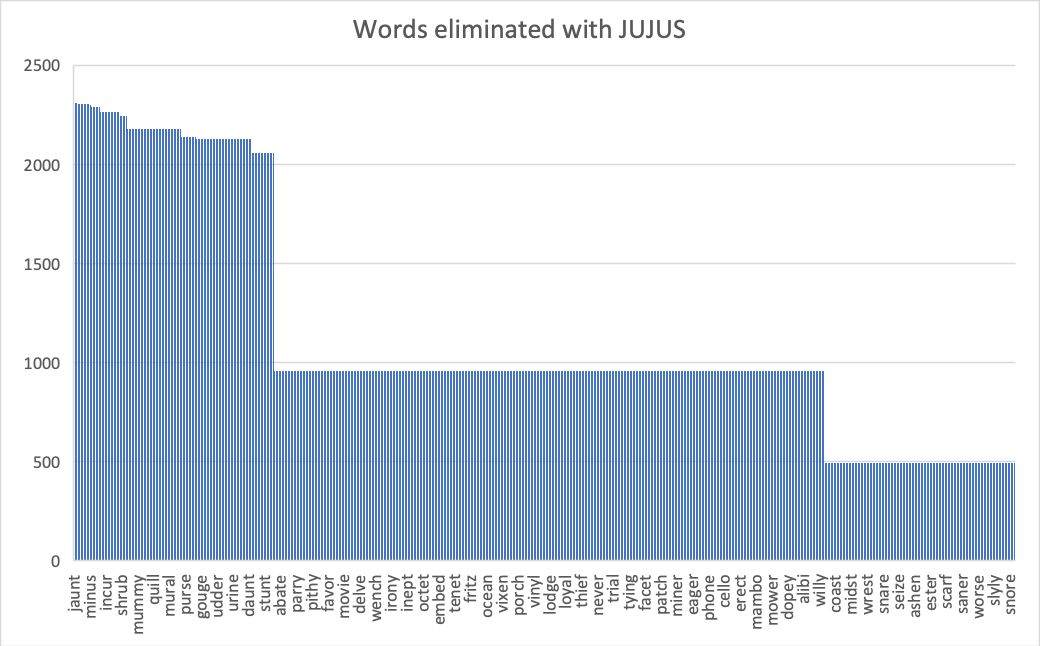
On the other hand, JUJUS is one of the worst words to guess. The same graph plotted for this guess isn't as smooth. Intuition tells us that this is a bad guess: J and U are uncommon, and JUJUS has two. But sometimes you get lucky -- if the solution was JAUNT or GUESS, you could solve on the next guess! Of course, for a large class of solutions like SHAVE and ARTSY, you'll eliminate only 496 possible words.

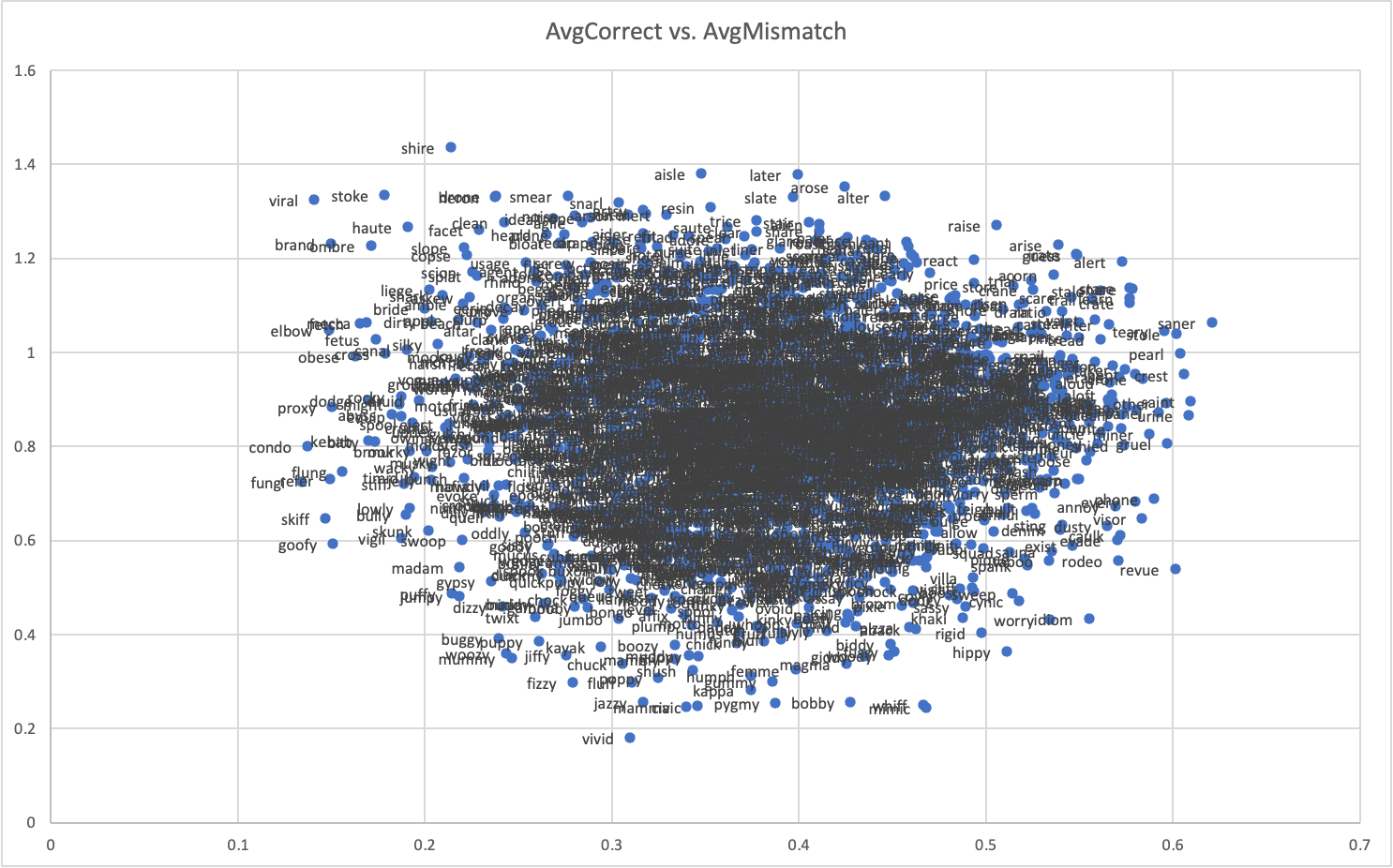
Drilling down into the average number of correct letters (in the correct position) vs. average mismatched letters, you can see that the best words are in the upper right quadrant and the worst words in the lower left.

I ran this strategy against randomly chosen words from the solution list. The strategy won 50/50 games, with an average of 4.42 turns per game. I'm sure with enough compute, and enough time, you could prove that every Wordle game is winnable in 6 turns.

There's also a Wordle hard mode. Under these rules, you must incorporate the information you're given – if you have a correct letter or mismatched letters, they must be present in each guess. This works against the strategy that the algorithm would play. The information is often not incorporated since guessing a correct letter again does not give any new information (only a chance to win the game).

Every hard mode game is not guaranteed to be won. If the hidden word is STORE, and "S" "O" "R" "E" are correct, you'll be forced to learn only one new letter at a time [SWORE, SCORE, SPORE, SHORE, SNORE]. Essentially, guessing each time. While I haven't empirically looked at it, I would assume that the original strategy still holds – try to eliminate as many words as possible.