Learning group theory through a simple example. No math knowledge needed.
Start with a triangle with vertices labeled 1,2,3, starting from the top and going clockwise. You can perform two functions on the triangle – either a horizontal flip (f) or a clockwise rotation (r).
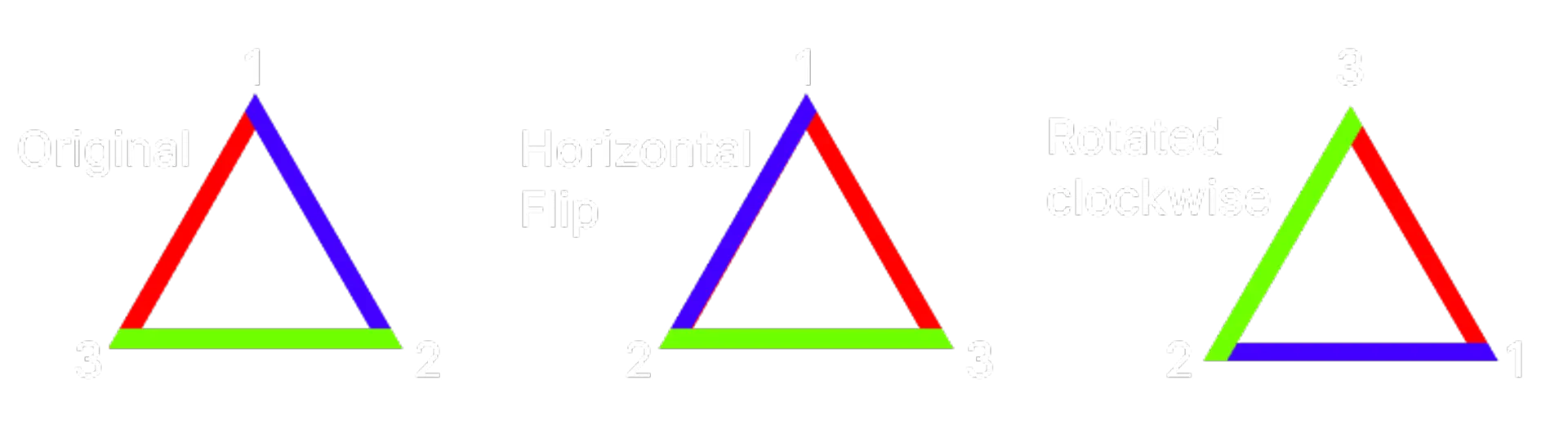
You can already see some patterns. For example, three rotations (let's use the notation rrr or _r_3) gives you the original orientation. Two flips (ff or _f_2) also gives you the original orientation.
Can you generate all possible orientations of the triangle only using horizontal flips and clockwise rotations? Hint: there are 6.
Try it on a piece of paper.
Some other interesting properties you might have found:
- Given any orientation, you can always do a series of flips and/or rotations to bring you back to the original.
- Harder, but "rearranging the parentheses" doesn't matter. These two function compositions give the same triangle: f(rr) and (fr)r.
With just flips and rotations, you can generate all permutations of a triangle. Together, these elements make up a mathematical group (specifically the symmetric group S3).
Here's a diagram of the elements and functions. Because of the symmetry, it looks nice (you can do these for any symmetric group, they are called Cayley Graphs).
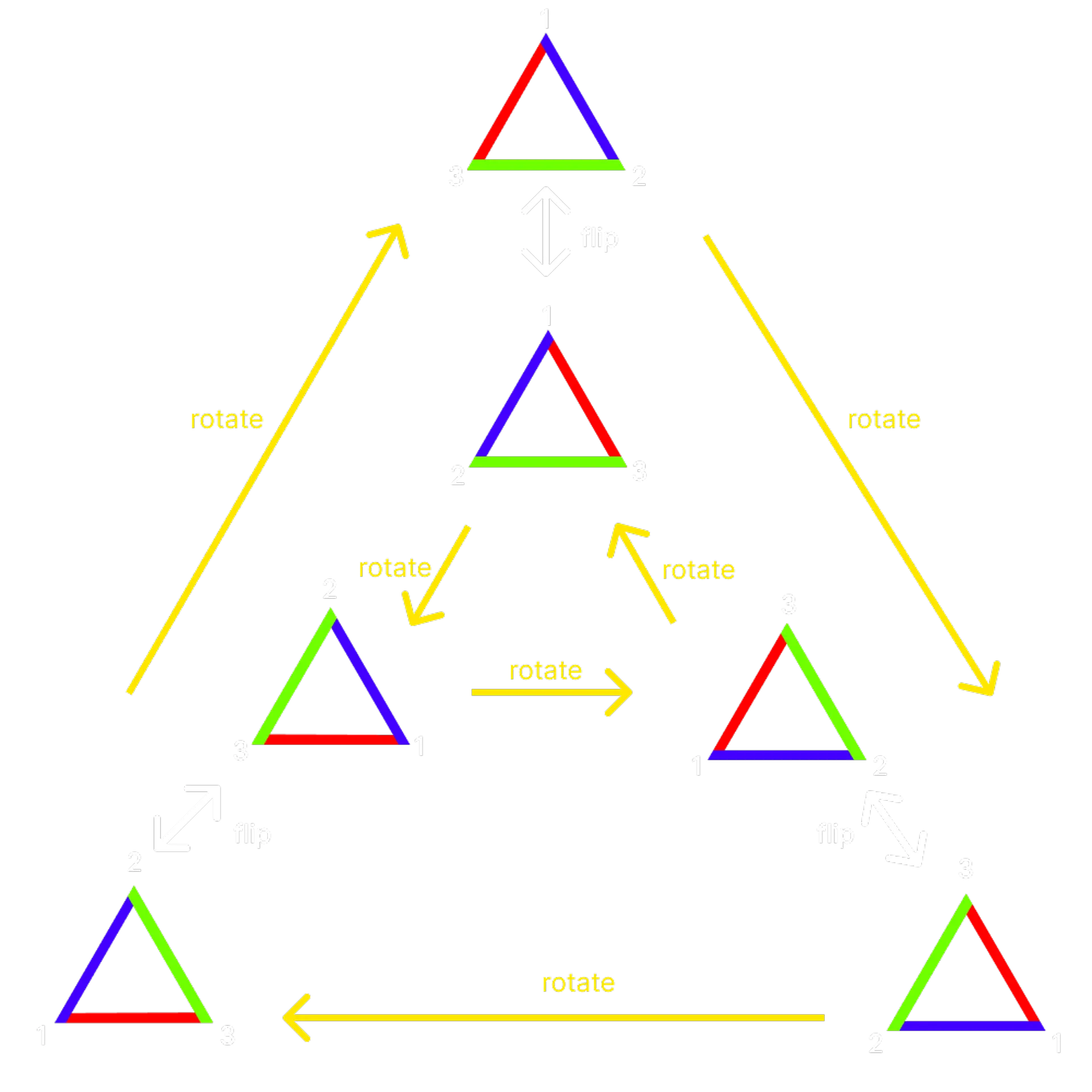
By doing this example, you've inadvertently proven the three axioms you need to show that this is a group.
The formal definition of a group and a short proof:
A group is a set G with a binary operation on G that satisfies these four axioms1:
- Associativity: For all a,b,c in G
(a • b) • c = a • (b • c) - Identity: There exists an element e in G such that, for each a in G
e • a = aanda • e = a - Inverse: For each a in G there exists an element b in G such that
a • b = eandb • a = e, where e is the identity element. - Closure: For each a, b in G,
a • bandb • aare contained in G.
For the symmetric group S3 above, let the elements be the triangle orientations expressed as flips and rotations: {1, r, f, r2, rf, r2f}. You can verify that these line up with the unique triangles in the diagram above. We use 1 as r__3 or s__2 because it is the identity element.
You can prove all the axioms above by observation since there are only six elements.
A more rigorous proof actually proves that all bijections (e.g., a permutation) from a set to itself form a group under function composition (a small example of the Innovator's Paradox!)
Other examples of groups:
- The set of positive and negative integers with addition (not multiplication – let
a = 2, there is no integer such that2 • b = 1(1/2 is not an integer). - The set of nonzero fractions ("rational numbers") under multiplication.
- The set of fractions under multiplication.
- The set of legal moves in a Rubik's cube.
Other fun group facts:
Number theory and cryptography make heavy use of groups. Elliptic curve cryptography uses an elliptic group.
We've completely classified all groups with a finite set of elements (the proof is over 10,000 pages long). There are 18 families of groups that have a simple pattern, and 26 that don't. Of those 26, there's a group that contains 20 of them (including itself) called the Monster Group. It has 808,017,424,794,512,875,886,459,904,961,710,757,005,754,368,000,000,000 elements.
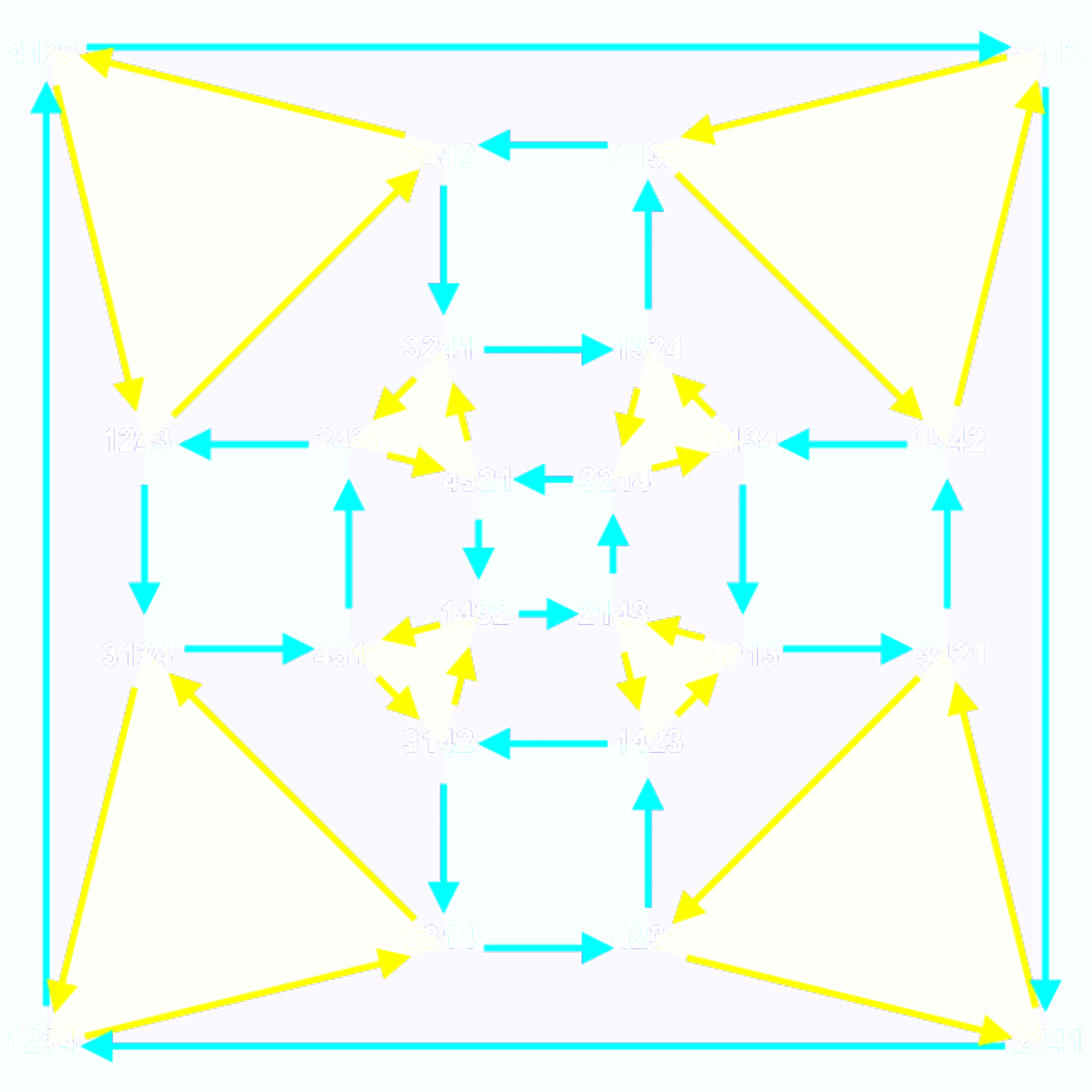
Cayley group of the symmetric group S4
1Usually denoted as three axioms, as the closure is given by the shorthand "binary operation on G", which implies G • G into G.