Ever wonder what's the mathematically "right" amount to bet? Want to know how many marbles to bet, so you don't get eliminated from Squid Games?
An engineer by the name of J. L. Kelly Jr. wondered the same thing at Bell Labs in 1956.
Kelly ended up with an equation for optimal betting — and promptly went to Vegas to test it with Claude Shannon (inventor of information theory) and MIT mathematician Ed Thorpe. Since then, investors like Warren Buffet have reportedly used it to size their bets. It's called the Kelly Criterion.
How does it work?
Kelly's criterion maximizes the theoretical maximum amount of wealth as the number of bets goes to infinity. You can look at this as optimizing the expected geometric growth rate, or the expected value of the logarithm of wealth. There's a rigorous proof that fits on a single page, but I'll spare you the details.
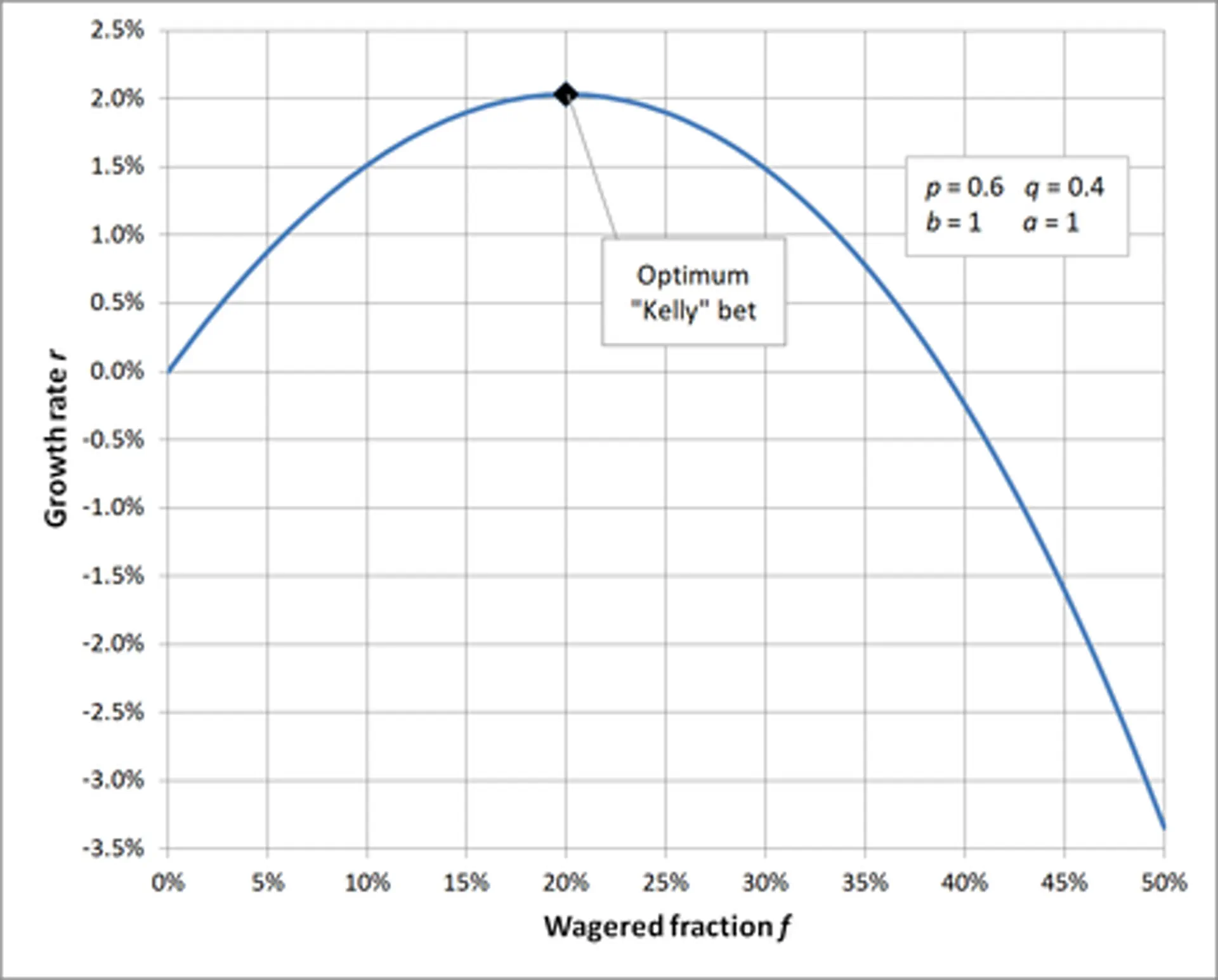
An Example
Let p be the probability of winning, and q be the probability of losing (p = q - 1). Then let b equal the amount that you gain with a win (your odds). This equation tells you f, the fraction of your current bankroll to wager.
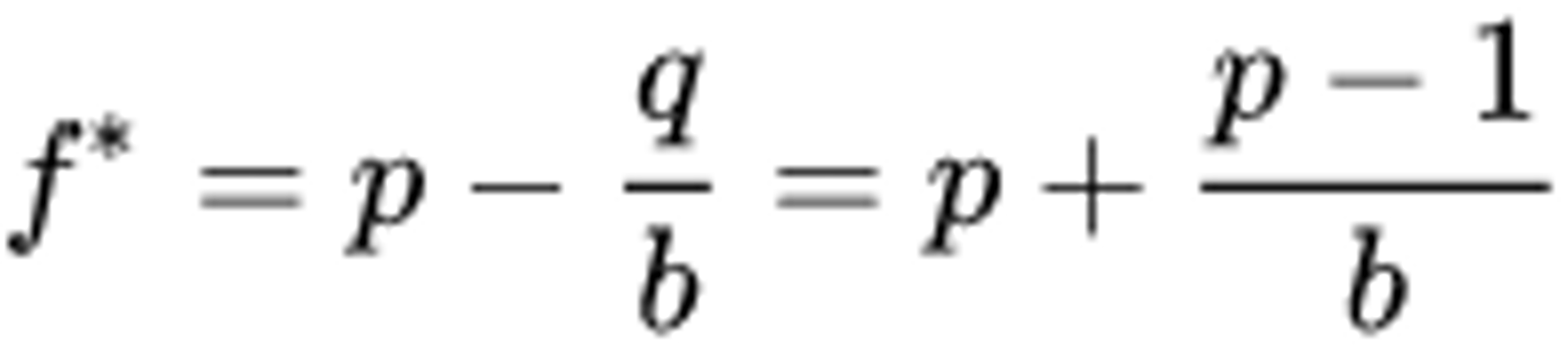
Let's say that you have a 70% chance of winning and you're given 2:1 odds. That means that p = 0.7 and b = 2*.* So you should bet 0.7 - (0.3) / 2 = 0.55, or 55% of your current cash as the optimal bet size.
Ok, but why isn't everyone rich?
Kelly's criterion is set up for an infinite number of bets, so it's meant for use "in the long run". Different constraints — like the utility of going bust — are often more important than achieving an optimal growth rate. Having a utility function — "how much is this money worth to me?" is important when applying the Kelly Criterion.
Some betters use the utility function in lieu of the odds in the Kelly Criterion, while others use only a fraction of the betting size suggested by the Kelly Criterion.