Sometimes, the world is not as random as it seems.
If I asked you what the leading digit in a list of the tallest buildings in the world, could you make a guess that's better than random?
Can you spot a fraudulent set of Bitcoin transactions just by knowing their amounts?
Surprisingly, the answer to both questions is yes. It turns out that for many real-life data sets, the leading digit is "1" about 30% of the time and "9" less than 5% of the time. Even more surprisingly, it holds regardless of the units used and whether or not the number system is base 10.
This result is known as Benford's law, and it's been used in court to prove cases of people providing fraudulent made-up numbers, most notably Enron's accounting fraud.
Benford's law: in many naturally occurring collections of numbers, the leading digit is likely to be small.
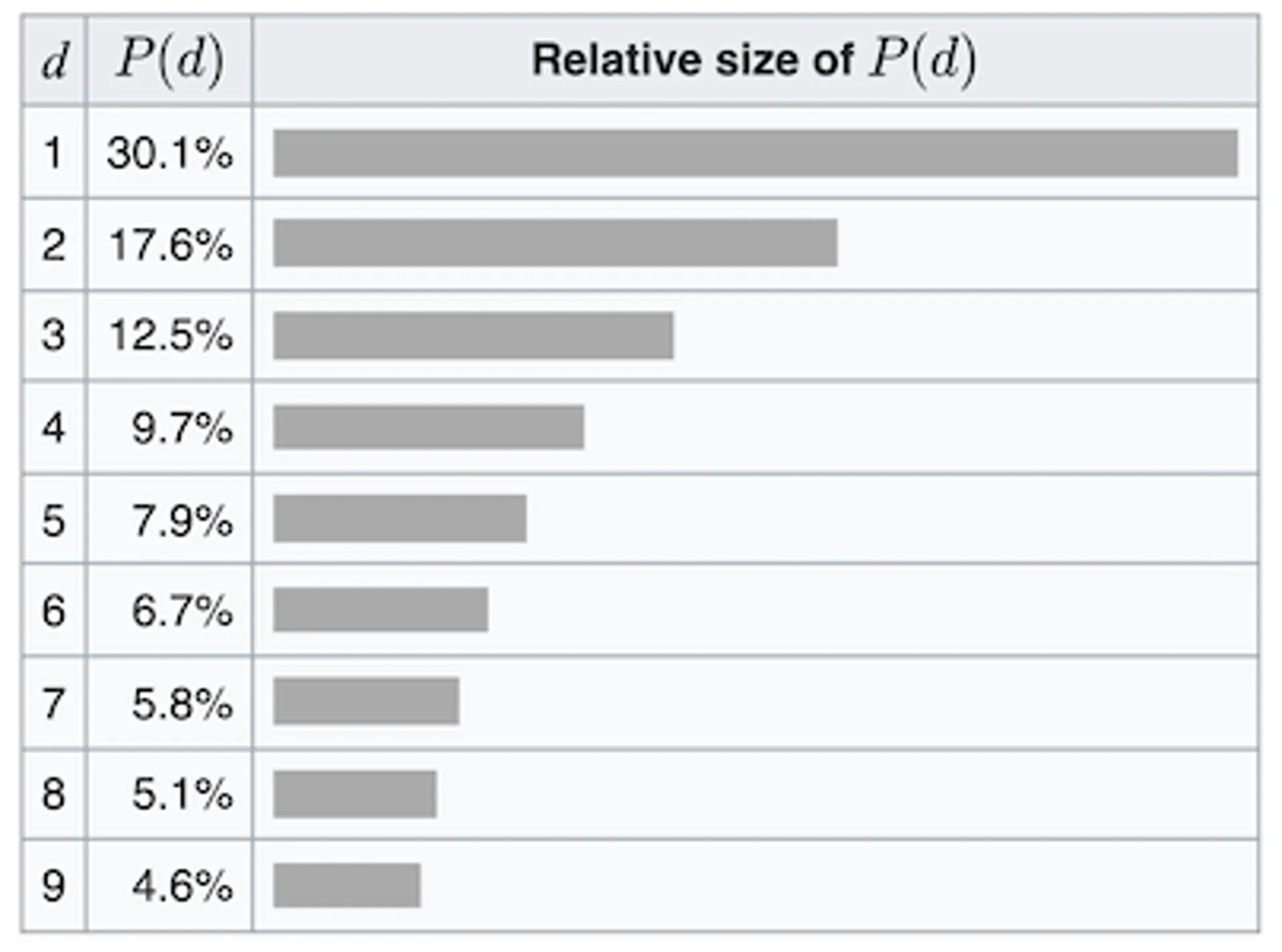
Benford's Law probability table from Wikipedia
Astronomer Simon Newcomb first discovered Benford's law (Stigler's law of eponymy). He noticed that the first pages of the logarithm tables in the back of his mathematics books were more worn than the other pages. Benford later tested it on 20 different data sets.
The data sets that follow Benford's law often span multiple orders of magnitude (which is why it doesn't apply to something like the heights of humans).
Some interesting distributions follow Benford's law: electricity bills, street addresses, lengths of rivers, death rates, populations, numbers that appear in newspapers, loan data, and stock market prices.
More recently, I came across a paper showing that fraudulent Bitcoin transactions could be spotted with Benford's law.
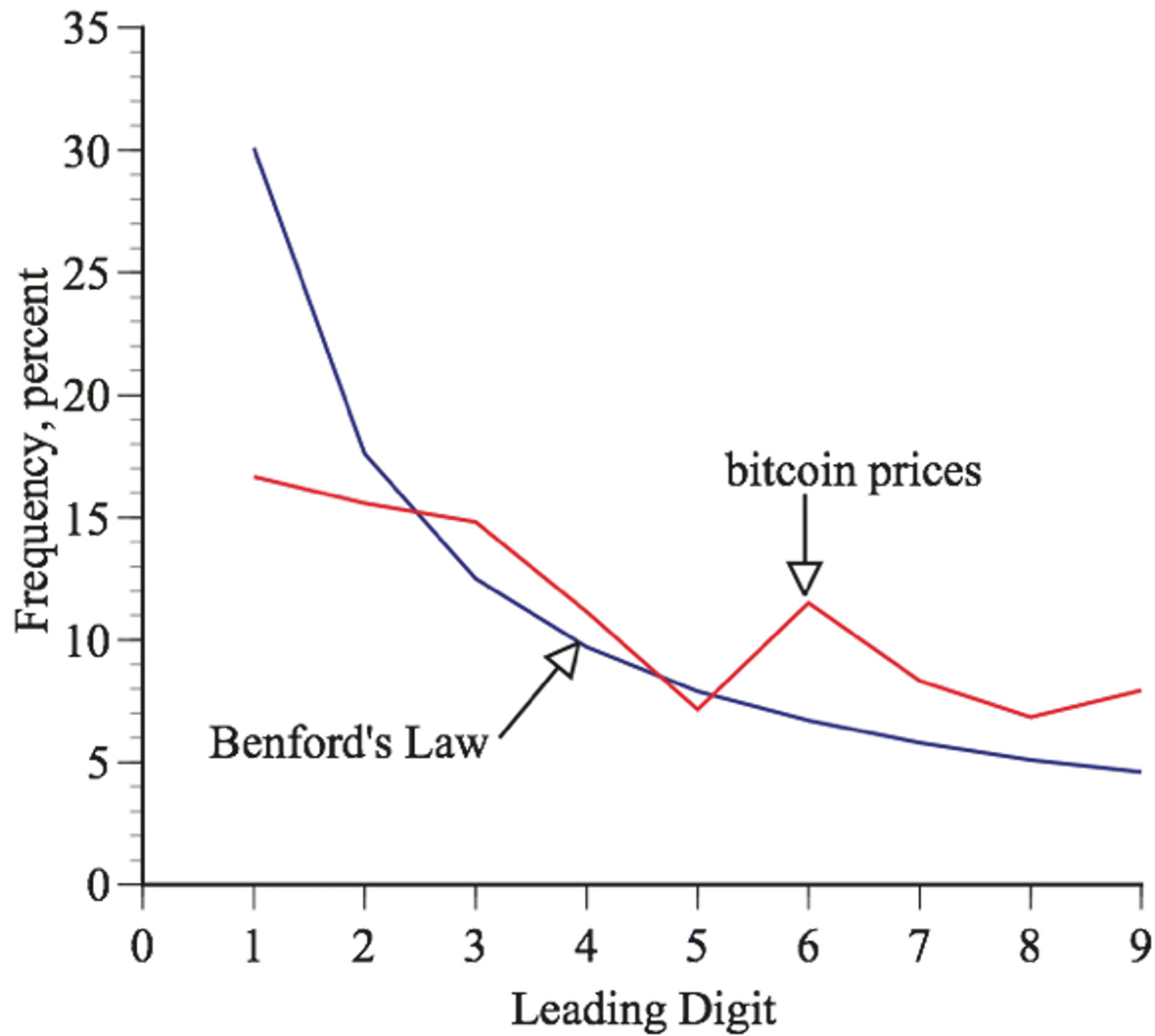
Benford's law is not a catch-all. It doesn't apply to all distributions. Most notably, distributions that don't follow Benford's law are ones with human bias (ending prices with $.99) or sequentially assigned numbers.
Benford's law is interesting because it's counter-intuitive. The observation came before Benford proved the theory. I seek results like Benford's law because they are a great reminder that my model of the world is woefully incomplete, that my intuition fails me sometimes, and that sometimes the world is not as random as it seems.