If you are to do important work then you must work on the right problem at the right time and in the right way. Without any one of the three, you may do good work but you will almost certainly miss real greatness.
Richard Hamming
No magic answer will guarantee that all three conditions are satisfied. But, by making a series of 95% confidence bets and gathering more data along the way, you can quickly find seemingly impossible futures.
A first principle cannot be deduced from any other axiom or assumption. First-principles thinking is about minimizing assumptions, and fewer assumptions mean less risk. So first principles thinking is intertwined with risk minimization. That makes first principles thinking a great decision-making framework.
We make better predictions with more data. Bayes' Theorem tells us how prior knowledge of conditions can affect the probability of an outcome. Machine learning models often do much better with more training data. First-principles thinking helps build a foundation by breaking down big decisions into a series of small but probable bets.
I didn't know what I wanted to do in undergrad and thought that anyone who thought they did was lying. But, I did know that STEM fields seemed to lead to more exciting outcomes - economists, physicists, mathematicians, computer scientists, and engineers. So, I studied mathematics for maximum optionality. I could always go from math to physics or math to computer science easier than in the other direction. It was a small bet, considering the optionality. So, I hedged with classes in philosophy, history, and the classics.
The possibilities were narrower after making that decision, but the choices were more straightforward. Where is the most important work happening? In the 1950s, the answer was physics, but now it's easily computer science.
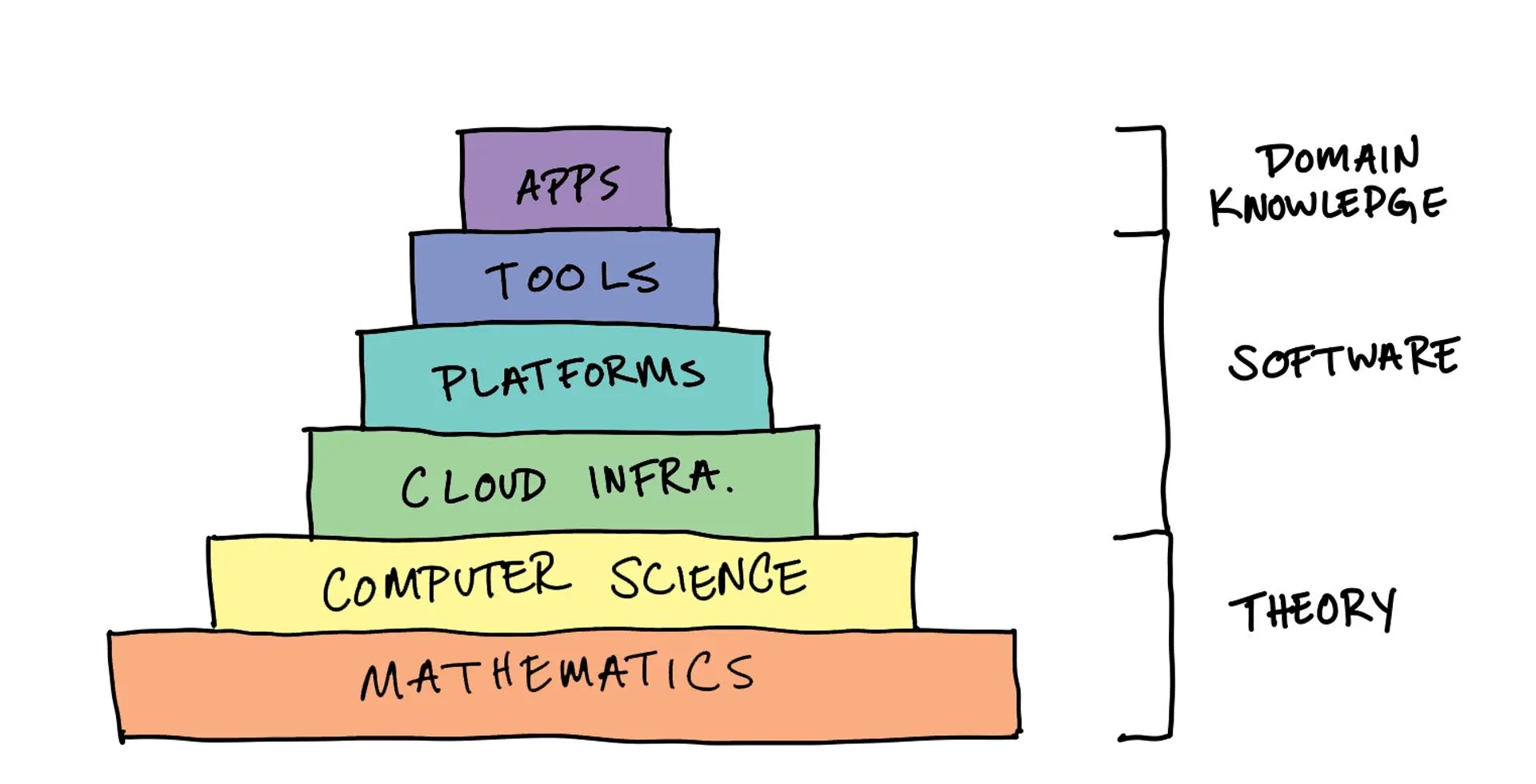
Within computer science, what is here to stay? Programming languages go in and out of style. However, algorithms, data structures, and abstractions seemed to be foundational knowledge. That's why I stayed as far away from taking classes that required programming, electing to learn that on my own instead. The riskier bet is to know what languages or frameworks will exist in the future, so focus on the theory.
With a foundation in mathematics and computer science, the paths again narrow. Now, hardware or software?
I made a bet on software. It has more leverage and optionality and is non-rival. In addition, I could iterate faster in software rather than hardware, trying and testing new paths to find important work.
To find specialization in software, I asked myself, what is obvious? One hypothesis that seemed obvious is that nearly all companies will utilize cloud computing somehow in the future. This statement may be obvious to many, but it has profound implications. Cloud also has high optionality. Cloud covers many areas of software - operating systems, networking, distributed computing, databases, machine learning, and pretty much every other subfield of computer science.
What's the next logical decision after cloud? As you get higher up the stack, the decisions become individually riskier. However, the cost of a wrong leaf decision is lower with the correct foundation.
A crucial part of Hamming's quote is getting the timing right. Decisions further up the stack have shorter half-lives (on the longevity of ideas, see The Lindy Effect). Platforms are the next logical step in my mind. Platforms are the act of codifying best practices into new abstractions. Gluing the building blocks together to make the theoretical model match the world. Unfortunately, platforms are more likely to be wrong, and the half-life is shorter.
But this is the benefit of foundational knowledge. A wrong bet can easily be pivoted into a correct guess the higher up the stack you are. You are still directionally right with the cloud if you pick the wrong platform. And the knowledge of what doesn't work is valuable in making future decisions. So you're increasingly less likely to choose the wrong paths.
The series of bets results in a thesis that many people could never get to without a foundation. So you can finally start answering, what do I know that nobody else knows? To others, the prediction will seem near impossible. But by first principles and foundational decision making, it will have been obvious.